Greek

 

Α history of the much discussed number e cannot start if we do not speak about logarithms in the first place.

In the 16^th – 17^th centuries an important development of the scientific knowledge occurred in all fields. The discovery of new lands, the circumnavigation of the Earth by Magellan and the development of sea trade caused the need of map production (Gerhard Mercator 1596). The introduction of Mathematics in Astronomy and Physics after Copernicus, Galileo and Kepler as well as the number of new data, which needed to be elaborated, required complicated calculations by the scientists. There was the need to invent ways that would free them from that burden. Since it’s easier to add than to multiply, a way of transforming addition into multiplication was invented, the logarithm.

 

John Napier (1550-1617), the 8^th Lord of Merchiston in Scotland, known for his books of religious content, was the first who, after having accepted the challenge of transforming a mathematical action into an easier one, observed the relation between the terms of a geometrical process and their respective exponents that follow arithmetical process.

Napier, using the number 1-10^-7 as a basis, suggested that each positive number N can be written as Ν=10⁷(1-10^-7)^L.

Thus we have the first definition of Neperian logarithm: L=Nap logΝ.

In the next 20 years he completed the successive terms of his geometrical process and finally presented them in his work Mirifici Logarithmorum Canonis Descriptio.

 

Note: We have here for the first time the rate of the sequence 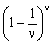, when ν is too big, as a base for logarithms.

 

Money is Mathematics

In the 17^th century an anonymous trader or usurer noticed a strange behaviour of the interest increase during bank transactions based on compound interest with annual interest divided into ν equal parts, when number ν is too big. Let’s follow the phenomenon:

The usual banking method of borrowed capital increase is:

 

Compound interest

If we deposit € K into an account giving ε % annual interest and this is repeated each year:

At the end of the 1^st year: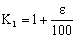

At the end of N year: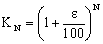

Another usual bank transaction is:

 

Compound interest ν times a year with annual interest divided into ν equal parts

That is, if we deposit € 100 into an account giving an interest 5% per year, we will have at the end of each year:

 

At the end of the 1^st year: € 105.00

If we deposit € 100 into an account giving an interest 5% per year, twice a year – at the end of each semester - we will have an interest of 2.5%:

At the end of the 1^st year: € 105.06

...At the end of each trimester, four times a year, we will have an interest of 1.66%:

At the end of the 1^st year: € 105.09

…At the end of each month, twelve times a year, we will have an interest of 0.416%:

At the end of the 1^st year: € 105.12

…At the end of each day, three hundred sixty five times a year, we will have an interest of 0.0137%:

At the end of the 1^st year: € 105.19

Suppose we have an interest ν times a year. For each period of conversion we consider as interest rate the annual interest rate divided by ν, that is %.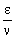

 

End of the 1^st year:

 

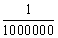
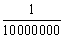
Note: The final capital for a very short period of conversion, e.g. / , does not exceed the 2.72 of the initial capital.

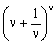
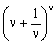
We notice that the formula approaches a rate without reaching it and this rate is number e. In that case, we say that the sequence in the formula has number e as a limit.

 

Number e as a limit

Number e is the limit of the sequence, as we noted.

But since for the high rates of ν the rate of will be almost zero,

we have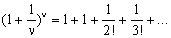

Consequently: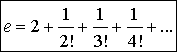

The quadrature of the hyperbole

Gregorius de Saint-Vincent (1584-1667) in his effort to square the hyperbole notes that, if the x and y coordinates of the graphic function are changing in a geometrical process, then the area between the axis of the coordinates and the hyperbole is changing in an arithmetic process.

 

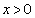
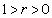
If and

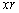
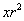
If the coordinates x, , , follow a geometrical process, the areas

Ε1=1 – r ,

Ε1+E2=2(1 – r),

Ε1+E2+E3=3(1 – r)…follow an arithmetic process.

So, we conclude that the area between the axis of the coordinates and the hyperbole is calculated by the logarithmic function.

 

When e meets φ: Logarithmic helix

Jakob Bernoulli (1654-1705) studied the logarithmic helix and he named it spira mirabilis because of its mathematic qualities, which make it the most popular decorative motif apart from the circle.

Logarithmic helix is described as a curve starting from a point (the pole) and twisting in a way that the distance between its points from the pole increases in a geometrical process, since the rotation angle increases in an arithmetic process. Each line passing through the pole incises the helix under the same angle.

 

Due to the fact that the logarithmic helix can be inscribed within harmonic rectangles (the ratio of their sides equals number φ), it is classified among the harmonic curves.

Logarithmic helix is one of the curves that can be seen very often in nature.

 

Bibliography

· Maor Eli, e: The Story of a Number. Cambridge: Cambridge University Press,1994;

· Eves Haward, Great moments in Mathematics - After 1650. Mathematical Association of America,1983;

· http://en.wikipedia.org/wiki/E_(mathematical_constant);

· http://www-history.mcs.st-andrews.ac.uk/history/index.html;

· http://mathworld.wolfram.com/e.html.

 

Greek